두 점을 이용하여 각도(기울기)를 구하는 방법

 

프로그램을 하다가 보면 두점을 이용하여 각도를 구해야하는 일이 있습니다. 이런 경우 어떻게 해결 할 수 있는지에 대해 알아 봅니다. 아래의 그림과 같은 개념의 문제 입니다.  한쪽 점이 들려서 올라간 형태에서 얼마나 수평선에서 각도가 발생했는지를 구하는 문제 입니다. 아래 같은 개념은 어떤 물체가 기울어진 정도를 구할때 적합하다고 할 수 있습니다.

 

 

예를 들어 자동화 검사 시스템에서 비전 시스템을 적용하여 기울기를 보정하는 경우 적용해볼 수 있겠습니다.

두점 사이의 각도

 

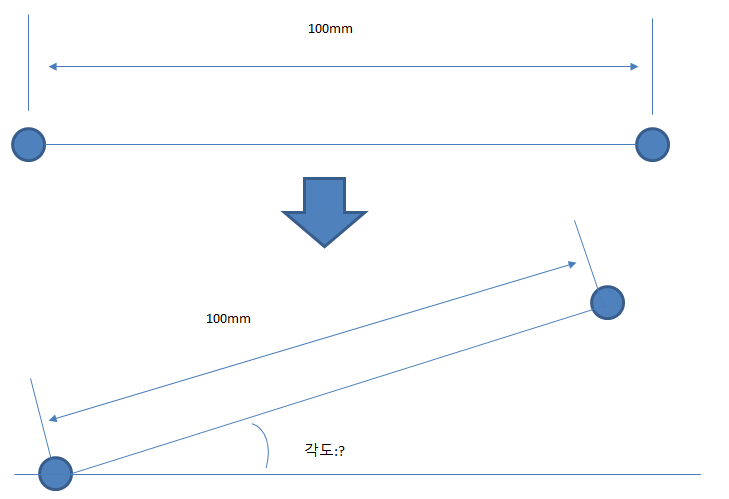
해결 방법은 우선 두점 사이의 거리를 기본적으로 알아야 합니다. 그리고 각점에서 좌표계를 적용하여 서로 얼마의 x,y를 가지는지를 확인합니다. 한점을 우선 0,0으로 적용한다면 아래 그림처럼 적용 해볼 수 있습니다. 결국 거리와 각 점의 좌표점을 알아야 합니다.

 

두점사이의 각도 좌표계 적용

 

 

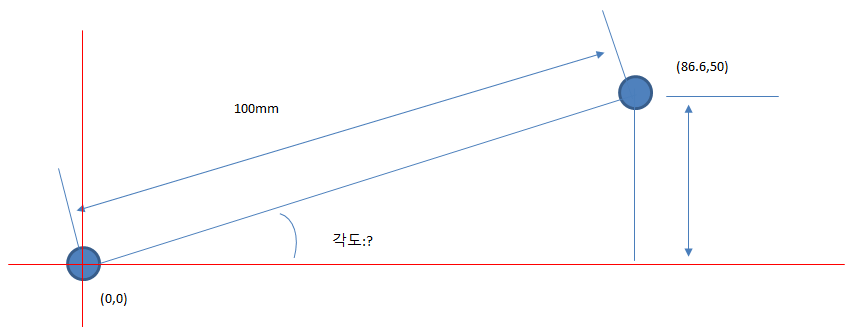
결국 위 그림처럼 삼각형이 나오게 되고 결국 삼각함수를 적용해야 한다는 것을 대략 느낌적으로 알 수 있습니다.

수식은 아래와 같습니다.

x = 한점을 원점으로 정한 두번째 점의 x 값

y = 한점을 원점으로 정한 두번째 점의 y 값

PI = 원주율

 

Atan2(x,y)*180/PI 

 

수식을 적용해 보면 결국 

 

x= 86.6

y = 50

PI = 원주율 (3.14)

 

결과는 약 30도 정도가 나옵니다.

 

 

위 그림처럼 두점사이의 좌표와 Atan2 수식을 활영하여 간단하게 기울기를 계산 할 수 있습니다. Atan2를 이용하면 좌표에서 각도를 쉽게 구할 수 있습니다. 

 

실제 제가 적용한 프로젝트의 예를 들어 보면 제품의 기울기에 특징적인 마크점을 이용하여 카메라로 촬상하여 이미지에서 좌표를 구한 경우 입니다. 

 

위 그림처럼 카메라 촬상범위 1,2를 정한 후 로봇을 이용하여 카메라를 이동하여 각각 포인트 점의 좌표를 구하여 제품의 기울기를 측정할 수 있습니다. 이외에도 다양한 영역에서 응용이 가능하다고 생각합니다.